Overview
This paper studies the training-testing discrepancy (a.k.a. exposure bias) problem for improving the diffusion models. During training, the input of a prediction network at one training timestep is the corresponding ground-truth noisy data that is an interpolation of the noise and the data, and during testing, the input is the generated noisy data. We present a novel training approach, named MixFlow, for improving the performance.
Our approach is motivated by the Slow Flow phenomenon: the ground-truth interpolation that is the nearest to the generated noisy data at a given sampling timestep is observed to correspond to a higher-noise timestep (termed slowed timestep), i.e., the corresponding ground-truth timestep is slower than the sampling timestep.
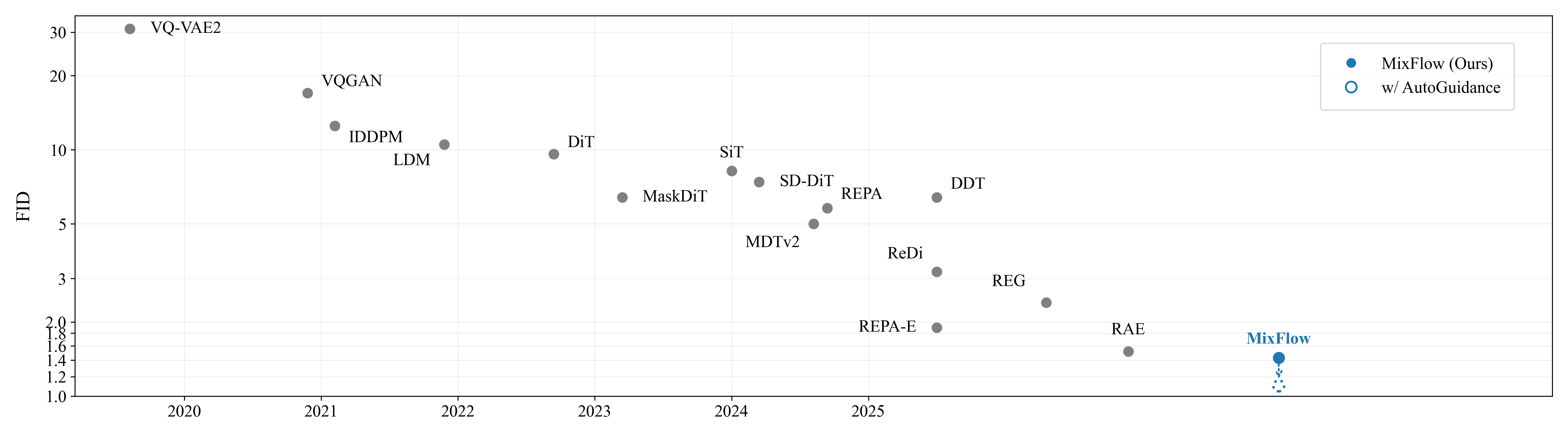
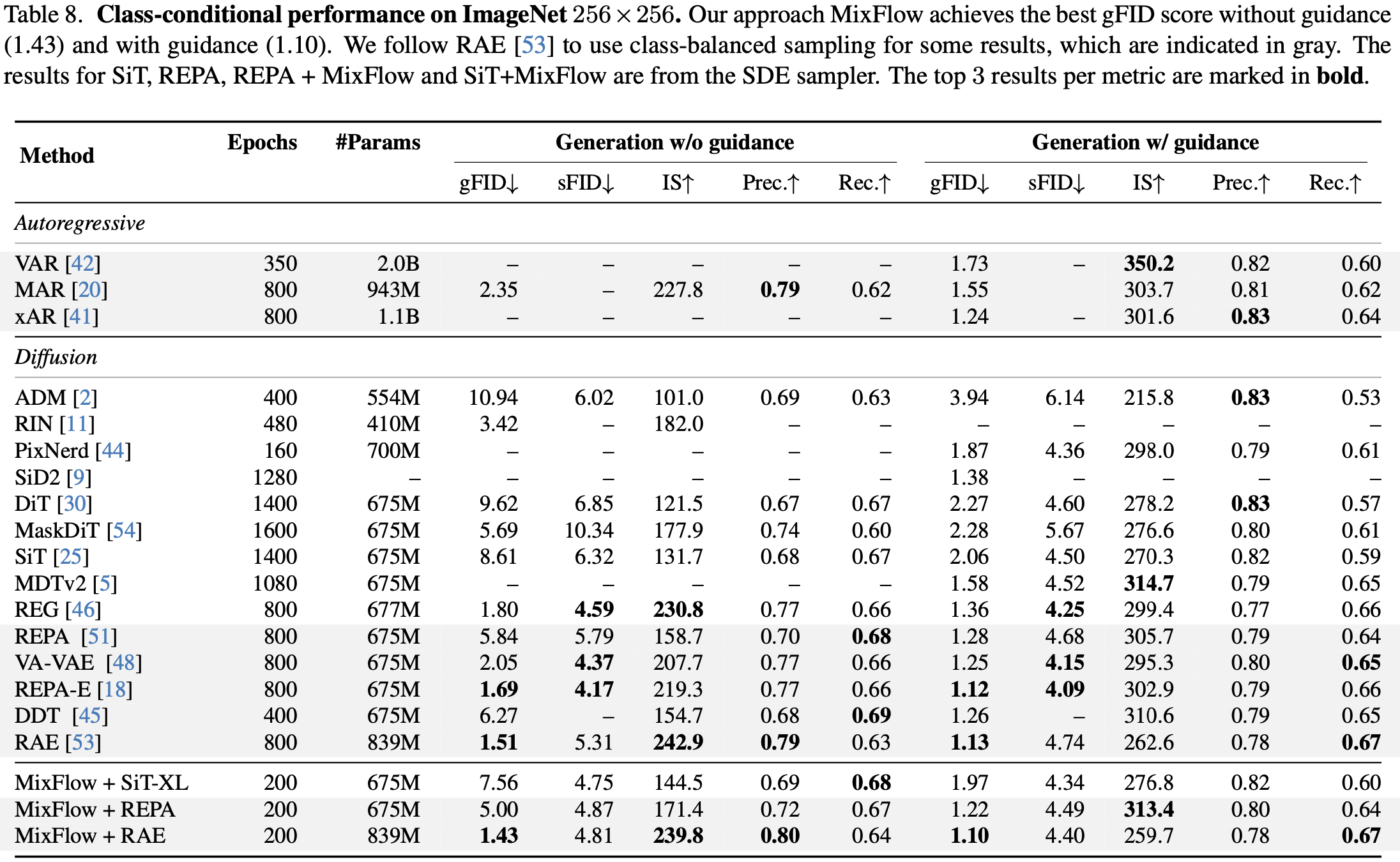
MixFlow leverages the interpolations at the slowed timesteps, named slowed interpolation mixture, for post-training the prediction network for each training timestep. Experiments over class-conditional image generation (including SiT, REPA, and RAE) and text-to-image generation validate the effectiveness of our approach. Our approach MixFlow over the RAE models achieve strong generation results on ImageNet: 1.43 FID (without guidance) and 1.10 (with guidance) at 256 x 256, and 1.55 FID (without guidance) and 1.10 (with guidance) at 512 x 512.
Slow Flow phenomenon
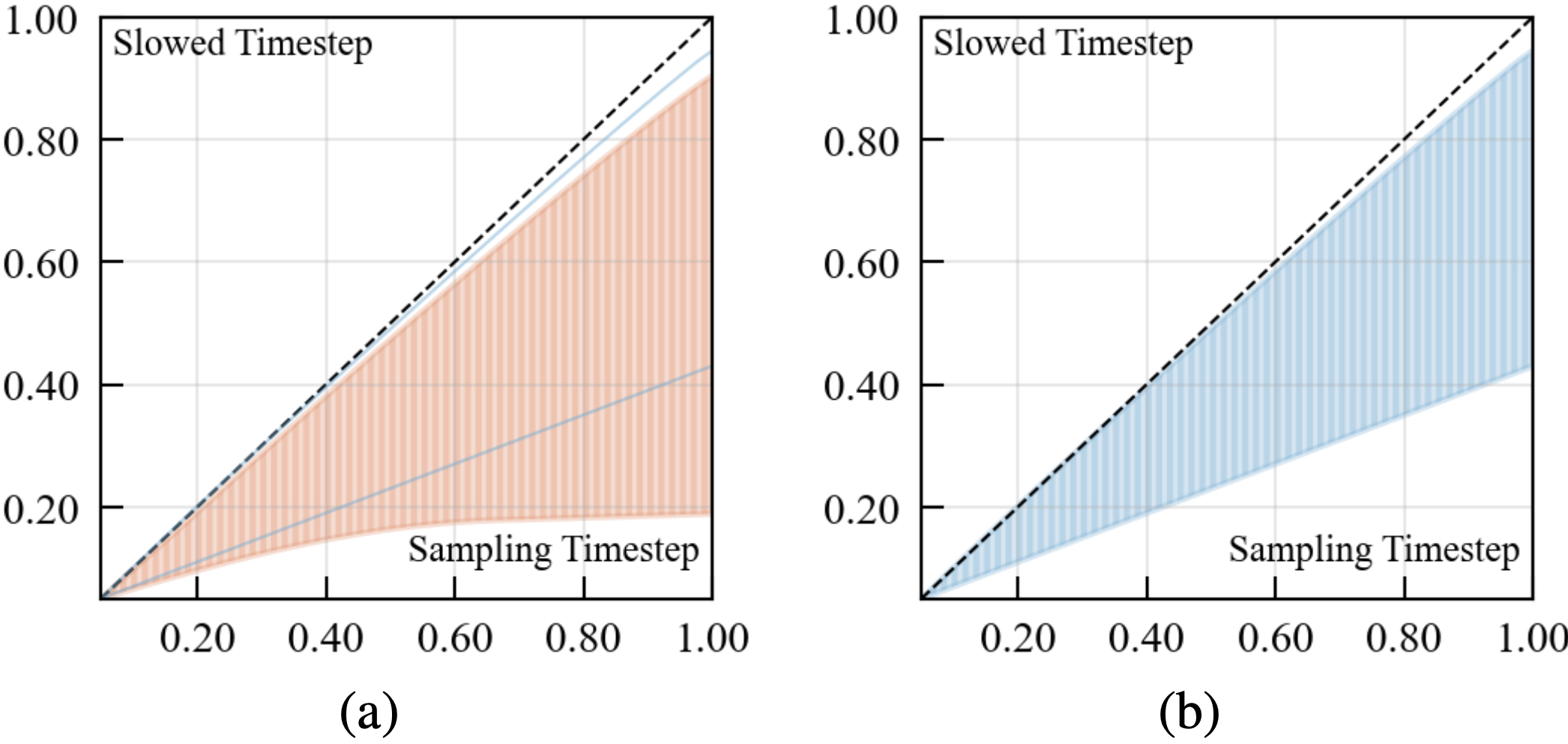
Illustrating (1) the Slow Flow phenomenon during the sampling process: the timestep (y-axis), corresponding to the ground truth noisy data that is the nearest to the generated noisy data at the sampling timestep \( t \) (x-axis), is slower (with higher noise), i.e., the shading area is under the line \(x=y\); and (2) the effectiveness of MixFlow training: the range of slowed timesteps for MixFlow training is smaller and closer to the sampling steps than standard training, indicating that MixFlow training effectively alleviates the training-testing discrepancy.
MixFlow
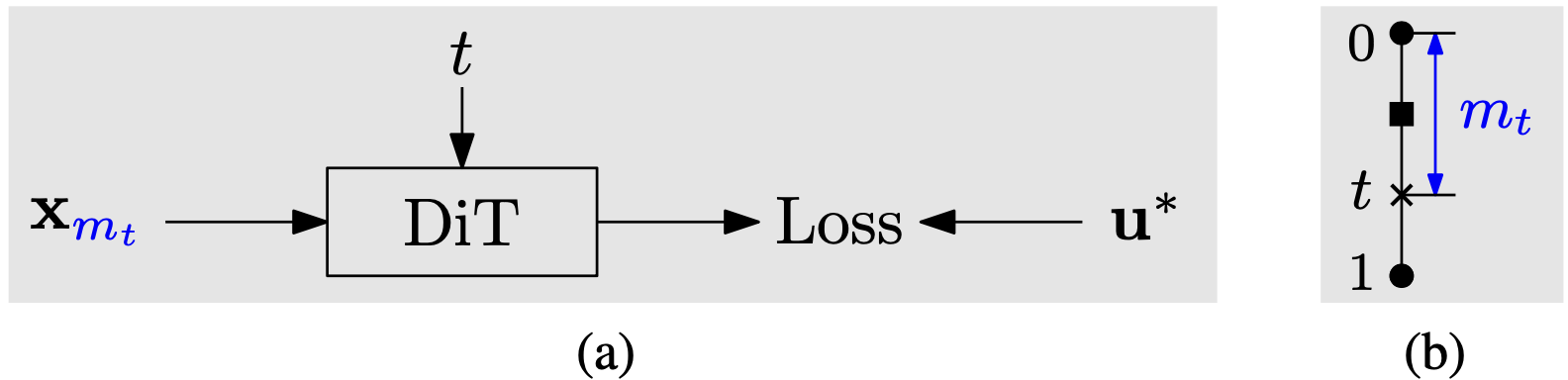
MixFlow samples the training timestep \(t\) from a Beta distribution \(\operatorname{Beta}(2,1)\), and samples the slowed timestep \(m_t\) from a uniform distribution \(\mathcal{U}[(1-\gamma)t, t]\). The prediction network is post-trained on the slowed interpolation mixture at each training timestep to reduce the training-testing discrepancy.
Easy Implementation
Only 5 lines of code are modified to integrate MixFlow into the RAE implementation. Concretely, we update two functions in transport.py. Left: RAE; Right: MixFlow + RAE.
Sample function
def sample(self, x1):
"""Sampling x0 & t based on shape of x1 (if needed)
Args:
x1 - data point; [batch, *dim]
"""
x0 = th.randn_like(x1)
dist_options = self.time_dist_type.split("_")
t0, t1 = self.check_interval(self.train_eps, self.sample_eps)
if dist_options[0] == "uniform":
t = th.rand((x1.shape[0],)) * (t1 - t0) + t0
# ...
t = t.to(x1)
t = self.time_dist_shift * t / (1 + (self.time_dist_shift - 1) * t)
return t, x0, x1def sample(self, x1):
"""Sampling x0 & t based on shape of x1 (if needed)
Args:
x1 - data point; [batch, *dim]
"""
x0 = th.randn_like(x1)
dist_options = self.time_dist_type.split("_")
t0, t1 = self.check_interval(self.train_eps, self.sample_eps)
if dist_options[0] == "uniform":
t = th.rand((x1.shape[0],)) * (t1 - t0) + t0
# ...
# Sample t from Beta(2,1)
t = 1 - th.sqrt(t)
t = t.to(x1)
t = self.time_dist_shift * t / (1 + (self.time_dist_shift - 1) * t)
return t, x0, x1Training Losses function
def training_losses(self, model, x1, model_kwargs=None):
"""Loss for training the score model
Args:
- model: backbone model; could be score, noise, or velocity
- x1: datapoint
- model_kwargs: additional arguments for the model
"""
if model_kwargs == None:
model_kwargs = {}
t, x0, x1 = self.sample(x1)
t, xt, ut = self.path_sampler.plan(t, x0, x1)
model_output = model(xt, t, **model_kwargs)
B, *_, C = xt.shape
assert model_output.size() == (B, *xt.size()[1:-1], C)
terms = {}
terms['pred'] = model_output
if self.model_type == ModelType.VELOCITY:
terms['loss'] = mean_flat(((model_output - ut) ** 2))
else:
# ...
return termsdef training_losses(self, model, x1, gamma=0.4, model_kwargs=None):
"""Loss for training the score model
Args:
- model: backbone model; could be score, noise, or velocity
- x1: datapoint
- model_kwargs: additional arguments for the model
"""
if model_kwargs == None:
model_kwargs = {}
t, x0, x1 = self.sample(x1)
# Remove the standard interpolated xt
t, _, ut = self.path_sampler.plan(t, x0, x1)
# Sample slowed timestep mt
mt = t + th.rand_like(t) * gamma * (1 - t)
# Compute slowed interpolation
_, xt, __ = self.path_sampler.plan(mt, x0, x1)
model_output = model(xt, t, **model_kwargs)
B, *_, C = xt.shape
assert model_output.size() == (B, *xt.size()[1:-1], C)
terms = {}
terms['pred'] = model_output
if self.model_type == ModelType.VELOCITY:
terms['loss'] = mean_flat(((model_output - ut) ** 2))
else:
# ...
return termsResults
Visualization
MixFlow generates high-fidelity images with fine-grained details and textures.

Class-conditional image generation
Post-training prior SOTA class-conditional models (SiT, REPA, RAE) with MixFlow improves ImageNet gFID to 1.43 (no guidance) and 1.10 (with guidance) at 256 x 256, and 1.55 / 1.10 at 512 x 512.
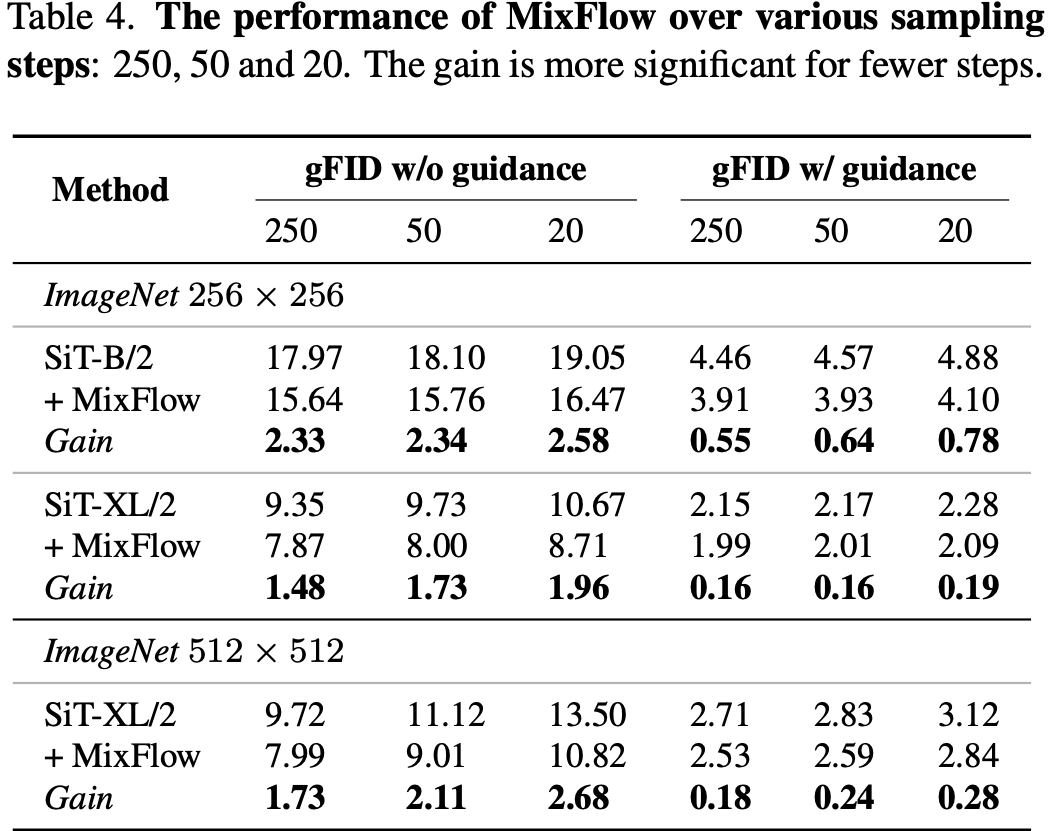
Various sampling steps
MixFlow yields larger gains when sampling steps are small, where Slow Flow is more pronounced and sampler approximation is coarser, reducing the training-testing discrepancy.
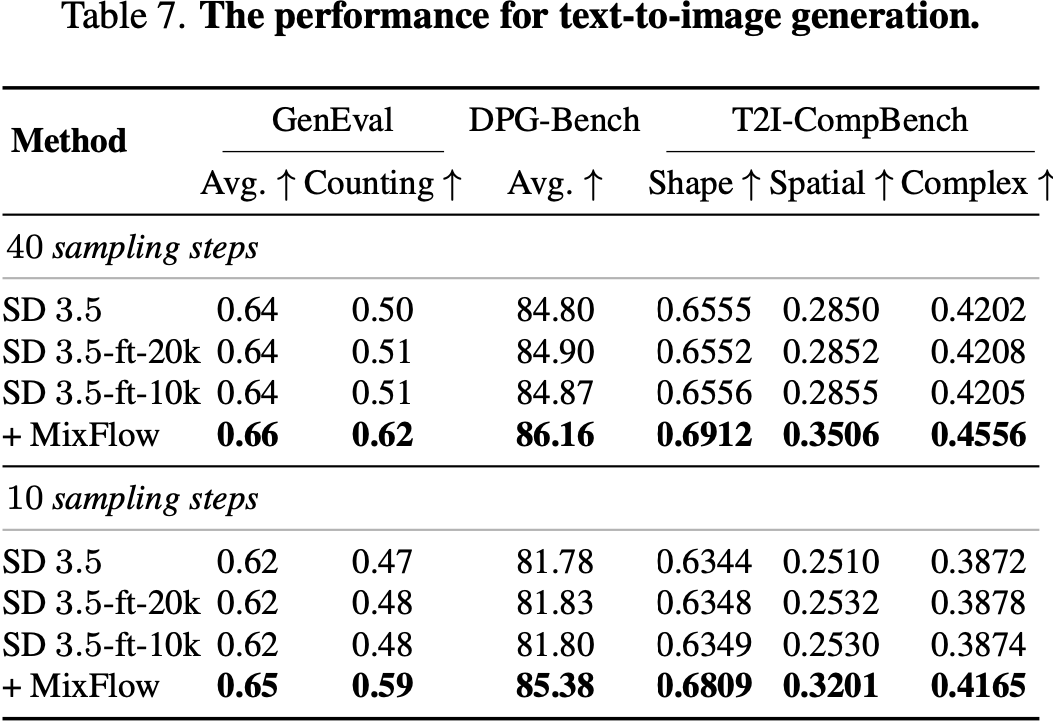
Text-to-image generation
Applying MixFlow to text-to-image diffusion models also boosts generation quality, showing the slowed-interpolation training generalizes beyond class-conditional settings.
Citation
@article{mixflow2025,
title={MixFlow Training: Alleviating Exposure Bias with Slowed Interpolation Mixture},
author={Hui Li and Jiayue Lyu and Fu-yun Wang and Kaihui Cheng and Siyu Zhu and Jingdong Wang},
journal={arXiv preprint arXiv: 2512.19311},
year={2025}
}